Загадки графики чисел

«Эти числа мерами сочти. Их линии умеют разделять

 жрецы.  Им маяки давали луч, как черта - аллею.

Шли у пар следы за призраками грёз.  И у края среза 

уже маячили узорами фигуры Божьи смысла и начала.

А их цепилиний брали из шкалы цифири…»

(Из отрезка числа Пи – 2 млн. 622-я тысяча цифр после запятой. Его расшифровка выполнена автором статьи).

О «свободе» чисел

Любые числа имеют внутренние невидимые свойства и способны самостоятельно выражать свою логику и смысл. Навязывание цифрам каких-либо правил и образов превращает их в «рабов» фантазий человека. Например, существует немало методик визуализации числа Пи с помощью цветных абстрактных картин. К каждой цифре прикрепляется один из 10 цветов. А их беспорядочное сочетание создаёт цветовое многообразие. Эти картины очень красивы, но они «мертвы». В них никогда не будет признаков разума или логики смысла.Если числам навязать какие-либо надуманные образы, получится тоже самое. В результате возникнут фантастические картинки,автором которых будет только человек.

Я не являюсь сторонником подобных методик. Мои исследования направлены на поиск ещё не раскрытых свойств чисел, в глубинах которых может находиться разумное начало. Функции чисел гораздо шире их математического применения. Например, в математике они подчиняются известным законам и правилам. А «свободные» знаки в константе начинаются после запятой.

Первые её 39 цифр могут определять точность вычислений.  А следующие за ними полностью покидают этот материальный мир и переходят в сферу абсолютной свободы духа. При этом все они будут умещаться в единице измерения, как символе вселенной.  В своих предыдущих статьях я приводил примеры  расшифровки чисел и нахождения в них  сведений об окружающем мире.Меня заинтересовал конкретный вопрос:может ли число выдавать разумные идеи языком графики? Я исходил из того, что каждой цифре соответствует реальная мера длины, выраженная в любых единицах измерения. Если перевести десятичную систему счисления (0 12 3 4 5 6 789 10) на длину цифровых отрезков, то получится следующий набор линий:

(0 .1__2____  3______ 4________5__________ 6____________7 ______________8________________9__________________10____________________).

Отдельная цифра 0 обозначена точкой, а все остальные – отрезками. Графика линий широко применяется архитекторами, художниками и конструкторами. С их помощью можно создавать форму и пространство.Если сложить столбиком параллельные линии различной длины, то на границах их окончаний образуется контур фигуры. Количество графических изображений будет безгранично, как и разнообразие чисел. 

В ходе отработки этой методики я убедился, что линии могут быть носителями разумной информации. А язык графики чисел образует своё визуальное информационное поле. Я подбирал расстояние между параллельными линиями  методом проб и ошибок. В результате оптимальной пропорцией оказалось число «золотого сечения» к единицам измерения (1:1,6). Например, при длине линий в сантиметрах, расстояние между ними будет 1,6 cм.

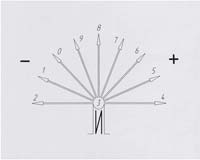
Если натуральный ряд чисел от 0 до 9 расположить симметрично по отношению к центральной вертикальной оси, то получится контур треугольника. Для его усиления нужно соединить концы линий правой и левой стороны.

В этой методике я использовал принцип симметрии. Все линии при построении делятся на две равные части по обе стороны от центральной оси. Примером является эта схема.  Рисунок № 1.

Симметрия является наиболее распространённой формой образования объектов материального мира. Например,у всех видов животных и насекомых правая и левая часть (в длину) одинаковы. Этому принципу «подчиняется» горбатый верблюд и сороконожка. То же самое наблюдается и у растений. Она гораздо привычнее восприятию человека, так как создаёт красоту и гармонию.

Симметрия в обществе проявляется в равновесии политических сил. К нему стремится любое государство и в целом человечество.  Диктат одной главной силы в мире является исключением из правил и не может быть постоянным.Против этого центра силы неизбежно возникнут противовесы. Равновесие частей любого объекта является законом мироустройства.

Кубок Пушкина

Этот принцип симметрии я стал применять при переводе чисел на графический язык. В качестве примера выбрал две даты, известные всему миру. Это цифры рождения (6 июня 1799 г.) и гибели А.С. Пушкина (10 февраля 1837 г.).Я решил узнать, что «говорят» эти два числа (661799 и 1021837) о гении русской литературы на графическом языке. И могут ли они как-либо «откликаться» на сущность событий? Боковые границы линий цифр первого числа, к моему удивлению, отчётливо показали контур кубка. Так он выглядит на рисунке №2.

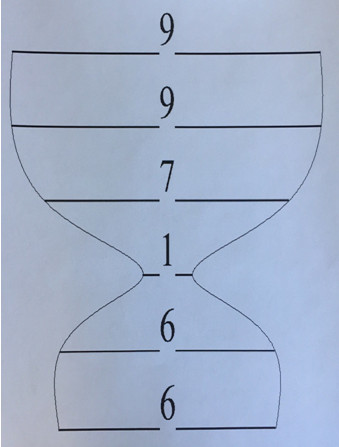
Кубок является символом духовности и бессмертия, а также особой почести человеку за его заслуги. В средние века их вручали рыцарям за победы на турнирах. У Пушкина было особое почтение к этому символу. Он неоднократно обращался к нему в своих произведениях. В стихотворении «Заздравный кубок» поэт предлагает поднять его за «Здравие славы», что на деле означает благодарение Богу за своё рождение и молодость. Например, дата рождения А.С. Пушкина встречается в первых 4-х млн. цифр числа Пи 12 раз после запятой.

Получается, что цифры «выразили» сам факт его рождения символом высшего отличия и почитания. И с первого дня предугадали» в нём будущую славу гениального мастера слова, непобеждённого никем по настоящее время.Перевод даты гибели А. Пушкина после дуэли с цифрового языка на язык графики показал контур светильника. Он выглядит так: рисунок № 3.

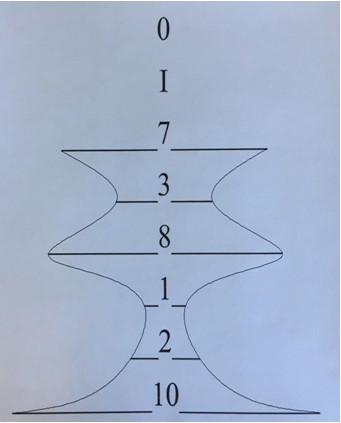Данный предмет упоминается в Библии 54 раза.  В ней говорится: «…радость наша исчезла, свет светильника нашего угас…» ЗЕзд 10:22.

Светильник является знаком светлого человека, границей его жизни и смерти. Гибель А. Пушкина воспринимается, как угасший свет гения поэзии. И эта горькая утрата никогда не будет восполнена.

«Угас, как светоч, дивный гений,

Увял торжественный венок.»

Написал М. Лермонтов в стихотворении «Смерть поэта».

Являются ли эти графические фигуры по отношению к поэту случайным совпадением? Эту загадку я объяснить не в состоянии.

С чего начинается константа?

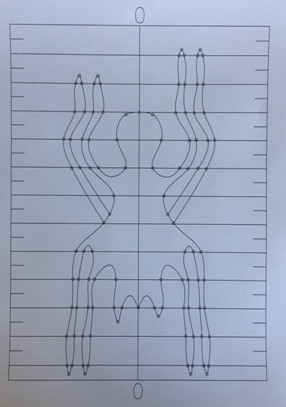
После этих исследований меня заинтересовала визуализация числа Пи с помощью набора и чередования параллельных линий. С этой целью я превратил первые 10 цифр константы после запятой (1415926535) в отрезки и сложил их по разработанной методике. На их границах у меня получился отчётливый контур человекообразной фигуры необычного вида. Предполагаемая форма её рук и ног никак не вписывалась в наши традиционные представления о человеке.Это видно на представленном мной рисунке № 4.

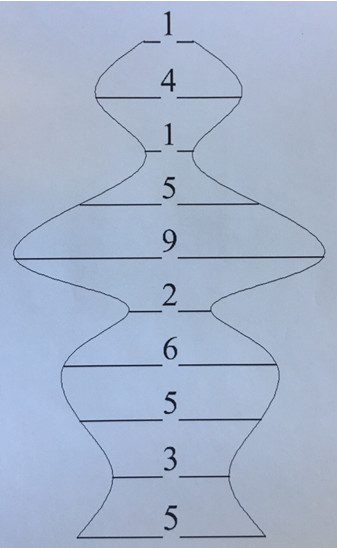Вначале я подумал, что цифры «допустили грубую ошибку» в построении человеческой фигуры. Что подобные контуры человека реально существовать не могут.Например, его нижняя часть определяет форму ног, кривизна которых зашкаливает. Я полагал, что такие ноги («колесом») могут быть лишь у людей-уродцев.

Угадывать самому их строение, означало бы «притягивание идеи за уши». Мне нужны были реальные факты и доказательства, что такая форма фигур могла существовать в богатой истории человечества.

С этой целью просмотрел в электронном виде все древние артефакты (фигурки и наскальные рисунки), сделанные руками народов мира. Мои поиски закончились удачей и доказательства были найдены.

В 1909 г. у села Мартыновка Черкасская обл. (Украина) местные крестьяне во время земляных работ случайно обнаружили клад из 116 серебряных изделий. В настоящее время его предметы хранятся в Музее исторических ценностей Киево-Печерской лавры. Учёные датировали находку 6-7 веками н.э. и относят её к Пеньковской археологической культуре древних славян.

Среди древностей оказались 4 одинаковые фигурки человечков, исполняющих танец. Представляю изображение одной из фигурок. Рисунок № 5.

Человек   исполняет танец с названием «присядка». Он мог быть распространён на территории древней Руси. Об этом танце имеются следующие исторические сведения:

Во времена Киевского князя Владимира Мономаха каменщик Пётр Присядка вытачивал изделия, находясь на корточках. Каждый день под вечер после работы он шёл на Крещатик и начинал подскакивать, разминая затёкшие ноги. Его странный танец заметил князь В. Мономах. Спустя пару дней Петро ежедневно исполнял эту пляску для самого князя во время завтрака обеда и ужина.

Эта русская народная пляска «присядка» исполняется в России и в настоящее время.

Нет сомнений в том, что эта фигурка «пляшущего человечка» 

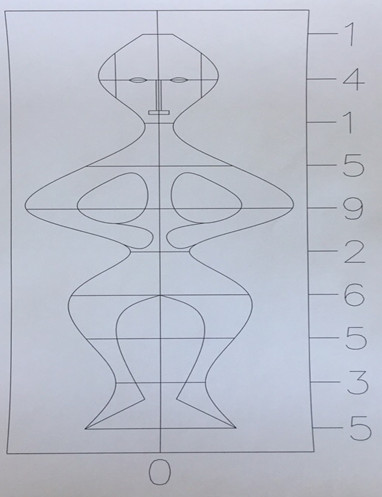очень похожа на изображение, обнаруженное мною в константе. Благодаря её «подсказке» я обозначил реальное положение рук и ног графической фигуры. Теперь она выглядит так: рисунок №6.

Танцующий человечек оказался единственным «творением» числа Пи среди 10 млн. цифр после запятой.

Приходится только удивляться, что константа начинается именно с этой фигуры.

Что это, совпадение или случайность? И на этот вопрос у меня нет ответа и, видимо, не будет.

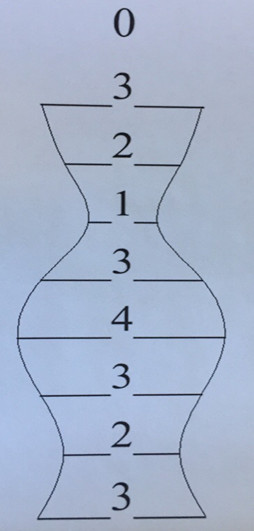Просматривая графический язык на других отрезках числа Пи, я обнаружил после 1 млн. 478 тысячи цифр после запятой число: (3 2 1 3 4 3 2 3), которое создаёт контур вазы классического образца. Привожу её изображение: рисунок № 7.

Природа не производит подобные предметы, поэтому любой человек не будет отрицать разумные идеи в этой графике линий. Их носителями являются цифры «свободного числа». В данном случае они проявляют себя на основе собственных свойств.

Цифры сами определили своими размерами линий её внешний вид. Я создал им лишь благоприятные условия, чтобы они могли проявить себя в этом «творчестве».

Если всё это не случайность и не совпадение, то возникает вполне резонный вопрос: что такое число и каковы его подлинные функции и возможности?

На службе у богов

  «Пустыня внемлет богу…»

М. Ю. Лермонтов

Занимаясь исследованиями возможностей графического языка чисел, я пришёл выводу, что их фигуры могут выполняться в любом масштабе единиц измерения. При этом их форма меняться не будет.

Например, фигура «пляшущего человечка», выполненная по такой же методике, в масштабе 1:300 (1 см. равен 3 метрам) на местности увеличится в длину примерно до 60 метров. И её можно будет легко заметить из космоса.

Подобный опыт уже существовал в древнем мире. Это создание индейцами больших рисунков (геоглифов) в пустыне Наска примерно 1500 лет назад.  Они были случайно обнаружены с самолётов в 30-е годы прошлого века.

Их реальный вид сверху выглядит так: рисунок №8.

Ранее я придерживался схожих взглядов при объяснении учёными этой таинственной загадки. Однако, после тщательного просмотра опубликованных рисунков,эти оценки у меня поменялись.

Представляю их копии: рисунок № 9.

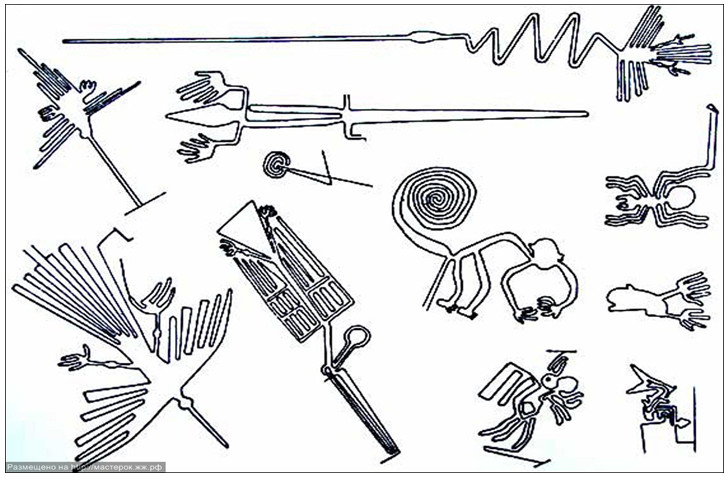
Моё внимание привлекла симметрия частей фигур к центральной оси и большое количество параллельных линий. Я увидел в рисунках язык чисел,выраженный в графике.Этими приёмами могли в совершенстве владеть жрецы древней цивилизации Наска. Применяя эту методику, они умели переводить свои эскизы рисунков в любой масштаб измерений на местности. При анализе достижений индейцев неизбежно возникают два вопроса:

1. Роль фигур в пустыне?

2. Технология их создания?

Исходя из своих представлений я попытаюсь ответить на эти вопросы:

1. Назначение рисунков

Отвергаю любую их связь с иноземными пришельцами. Если бы они действительно посетили Землю, то для местных аборигенов превратились бы в  богов, спустившихся с небес. Полагаю, что всё земное «творчество» древних жителей Наска было связано с религией язычества. Знаки земной графики стали для них одним из способов обращения к богам за милостью. Племена и родовые общины этой цивилизации искали связь с богами и духами, рассчитанную больше всего на их зрительное восприятие. Для небесных богов предназначались видимые рисунки, а для земных – полосы и линии. В течение тысяч лет формы почитания божеств постоянно менялись: от молитв до ритуальных действий и жертвоприношений.

Всё зависело от условий проживания и местных особенностей. В распоряжении древних индейцев Наска оказалась гигантская песчаная «доска», лишённая растительности. Эту уникальную природную площадку, как «земную ладонь», невозможно было не использовать для графических обращений к богам. Её общая площадь составляет около 500 квадратных километров. Среди изображений имеются разные виды линий и фигур, а также рисунки животных, растений и насекомых больших размеров. Они считали, что боги быстрее заметят крупные рисунки с высоты небес, чем мелкие послания. И за этот жертвенный труд будут благодарить жителей Наска хорошими урожаями.

Индейцы поклонялись священным птицам, «вестникам богов», которые с высоты своего полёта могли, как «в зеркале» увидеть свое изображение на земле.    Вся деятельность людей в цивилизации Наска определялась религией и ничем другим. Это был образ их существования. Все языческие обряды и ритуалы управлялись жрецами при очень строгой дисциплине. Они поклонялись многим животным (тотемам), считая их своими предками. И нашли способ сохранить память о них своими рисунками на тысячи лет. Всё что их окружало, считалось результатом деятельности богов и поэтому всячески почиталось.На плато не было изображений предметов и вещей, принадлежащих людям. И все рисунки в пустыне им не были предназначены. Поэтому выполненную работу, по их представлениям, могли оценить только боги.

2. Как сделать (технология)

Все линии и рисунки на плато Наска по своей сложности делятся на пять уровней:

1. Простые линии и полосы.

2. Геометрические фигуры (треугольники, прямоугольники, трапеции).

3 Спирали.

4. Животные и птицы.

5. Насекомые.

Для каждого вида работ была своя технология. На местности применялись разные способы измерений в создании фигур и линий. В работе использовались одни и те же инструменты. Это: измерительная верёвка, с нанесёнными делениями мер длины. Деревянные лопаты для выемки верхнего слоя грунта. Дополнительно к лопате мог применяться ручной  ударный инструмент (кайло) для обработки твёрдого грунта. Колышки для обозначения линий на площадке и камни для их забивания. Шест определённой длины для прокладки линий спиралей. Небольшие эскизы рисунков, с нанесёнными на них размерами расстояний (в единицах измерения).

Верёвки, пришедшие к нам из каменного века, выполняли две очень важные функции: 1. С их помощью проводили все измерения на местности. 2. Верёвка, в натянутом состоянии, создавала на поверхности земли прямую линию. Каждый математик подтвердит, что самая правильная прямая-это натянутая нить. Древние индейцы могли изготавливать верёвки из шерсти или кожи лам,которых разводили в достаточном количестве. Для применения этих инструментов нужны были лишь рабочие руки.

Жрецы управляли разметкой линий при создании фигур на плато.  Рисунки имели размеры от 50 до 290 метров. Они зависели от возможностей натяжения верёвки. Это был своего рода «рекорд». Трудно себе представить, чтобы верёвку можно было превратить в прямую линию на расстояние -0,5 км. Простые расчёты показывают, что верёвка длиной 300 метров могла весить до 100 кг. Например, современные рулетки со стальной лентой выпускаются длиной не более 50 метров. Иначе лента провисает и искажает размеры.

Остановлюсь на технологиях выполнения отдельных работ. Самая простая из них – это прокладка прямых линий в пустыне,которых около 13 тысяч.Все они имеют беспорядочные направления, без какой-либо системы. Для индейцев было гораздо важнее наличие самой линии,чем её направление. Для их прокладки ориентирами могли служить вершины гор, звёзды или точки восхода и захода солнца на горизонте. Эти лучи-линии и полосы предназначались для связи с земными богами и духами. Их «адреса» не были известны, поэтому «каналы связи» прокладывали наугад («на деревню дедушке»).

Каждая родовая община надеялась, что боги быстрее окажут им «адресную помощь» по этим прямым линиям-указателям. За столетия в пустыне образовалась целая «паутина» графических «линий связи» между жителями и богами. А само плато Наска стало самым древним в мире «коммутатором».

При проведении линий на местности выполнялись три вида работ тремя группами людей: Одна группа обеспечивала верёвкой прямые линии. Вторая забивала по этим линиям колышки (с промежутками около шага). Третья – вдоль колышек рыла канаву. Затем колышки и верёвка переносились на следующий отрезок. И всё повторялось по такой же схеме.

 Таким способом можно было проложить черту на земле на многие километры. При высоком мастерстве в выполнении этих работ, отклонение линии могло быть ничтожным. На следующем этапе индейцы научились соединять прямые линии друг с другом с помощью углов. И у них стали появляться на плато геометрические фигуры.

Спирали на местности создавались по другой технологии. Самая сложная часть - её центр. Он обозначался верёвкой, сложенной вдвое в виде большой петли и двумя параллельными линиями. Она изображала на земле «эскиз» первичного кольца спирали. Затем рисунок центра обозначался колышками и по их кольцу рыли канавку. После верёвку убирали и продолжали закручивать остальные кольца на одинаковом расстоянии между ними. Размеры определяли длиной шеста.

В создании рисунков птиц и животных применялись наиболее сложные технологии. Их суть заключалась в способах превращения маленьких этюдов в гигантские копии на местности. Чтобы создавать подобные рисунки нужна была центральная осевая опорная линия, равная длине фигуры.На рисунках её не видно, но эту ось применяли в обязательном порядке.

Ценность этой линии можно сравнить со столбом, на котором держится шатёр, или с уровнем моря по отношению к суше.  Эта ось соединяла в единое целое все части рисунка.Индейцы создавали прямую центральную линию натяжением длинной верёвки. Затем её обозначали колышками для поперечных параллельных измерений.

От этой оси («как от печки») справа и слева делались замеры всех расстояний до точек линии фигуры с помощью параллельных натяжений верёвок. Все проведённые замеры обозначались на местности колышками. Затем вдоль их пунктирных линий рыли канавки определённой ширины и глубины.Применялось разделение трудовых операций. Каждая группа людей выполняла свой участок и вид работы.

Самой сложной фигурой для них был рисунок паука длиной около 50 метров. Вот его реальный вид: рисунок № 10.

Для его изображения, по моим подсчётам, индейцам требовалось выполнить верёвками более 120 измерений от центральной ключевой линии.

Показываю примерный эскиз паука: рисунок № 11.

Родовая группа из 15-20 человек могла создать любой рисунок на плато за 5-7 дней. За всеми измерениями осуществлялся строгий контроль. История умалчивает с какой отдачей боги и духи воспринимали их земные «дары» и сигналы линий.

Чтобы окончательно поставить точку в этом таинственном достижении, нужно повторить  где-то в подобной пустыне то, что сделали жители Наска в глубокой древности.

Технология по созданию гигантских графических фигур на местности разработана во всех деталях и ждёт своего часа.

Автор: Владимир Кондряков