В тени чисел
«В числах все дела закрыты.
В них двери в тайники вели,
И шифры к их замкам забыты.
В пучках из цифр узлы вязали.
Там дух у хаоса плутал,
И вирши первые мужи искали.
А иероглифы к учёбе
Им жрец из храма начертал…»
(Текст взят из числа Пи – 7млн. 375-я
тысяча цифр после запятой)
Потусторонние числа
«Правая, левая, где сторона?»
(Из русского романса)
В числах содержится весь набор суждений о мироздании. Они являются духовным инструментом человека в познании и оценке окружающего материального мира, во всех его изменениях. Сама природа не имеет систем измерений. Их способы являются продуктом человеческого разума. Древний человек не сразу стал считать предметы. Он оценивал природу через свои ощущения. Его количественные преставления вначале определялись через простые понятия: больше – меньше; много - мало; короче – длиннее. Продолжительность времени он будет оценивать количеством затраченного труда. А свою силу – поднятием тяжестей.

Современная математика способна оценивать весь спектр материальных свойств, явлений и процессов, в том числе в обществе. Для проведения любых измерений в масштабе Вселенной ей хватит числа из ста знаков, или 10 в сотой степени. А для определения крайней точности – 39 знаков числа Пи после запятой. Все остальные наборы чисел будут находиться вне материального мира в своём применении. Их сферой действия является бесконечный духовный мир.
Его суть кроется не в первичности или вторичности появления по отношению к материи. Это начальная двоичная система построения мира. В этой связке наш материальный мир появился, развивался и совершенствовался по духовному коду развития. Источник духовности чисел не известен и никогда не будет разгадан. Их количественные, материальные проявления произошли из хаоса вместе с первым духовным сигналом.
Помимо реальных чисел для логического завершения существуют их дополнения десятичной системы. Я отношу их к потусторонним числам. Они являются тенью любых реальных цифровых последовательностей и ограниченно применяются в математике. Основой счёта является десятичная система, состоящая из 10 одинаковых частей. Их количество обозначается цифрами, которые имеют графическое и речевое отражение. В системе счёта каждая цифра больше предыдущей на единицу. Все остальные числа являются суммой этих единиц и десяток и имеют свои названия. На пути к числу 10 фиксируется любая из названных цифр и завершает его. Например, у цифры 7 до завершения не хватает 3-х единиц. Для числа 84, не хватает до ста 16 единиц, а для 748 не хватает до тысячи - 252.
Запись любых чисел ведётся слева направо. Арабы пишут тексты справа налево, а числа пишут в обратном направлении. Правая сторона недописанных до логического завершения чисел образует теневое число. На рисунке они показаны так:
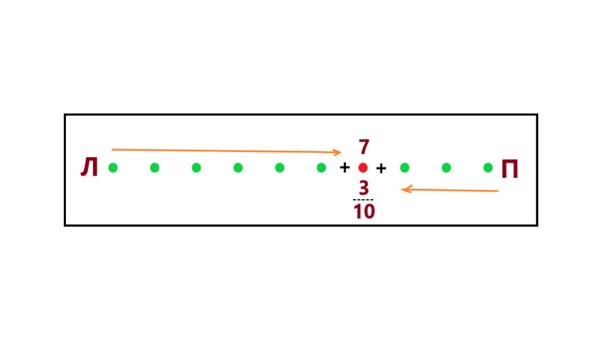
В его левой части отмечена цифра 7, а на правой стороне её продолжением является – 3. В сумме они образуют число 10. В центре этой схемы будет цифра 5, а её завершением – 0.
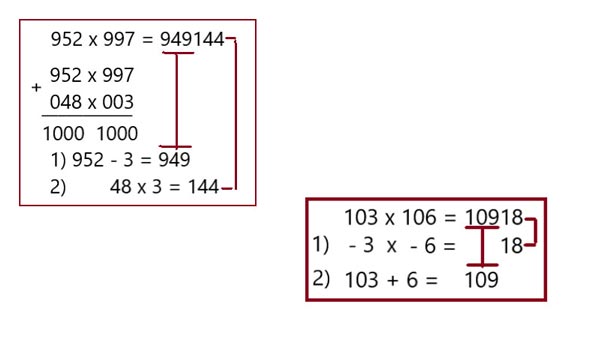
Реальные и потусторонние числа имеют ряд схожих свойств. У них одинаковая разница между соседними цифрами. При умножении любых реальных чисел их продолжения дают половину ответа. Например, можно совсем не учить таблицу умножения и заменить её простыми арифметическими действиями (см. схему). При умножении любых двузначных и более чисел схема решения такая же. Пример: 86 х 97 = 8342. Числу 86 до ста не хватает 14, а 97 – 3. Решение:
86 – 3 = 83 2) 14 х 3 = 42. Общий результат – 8342.
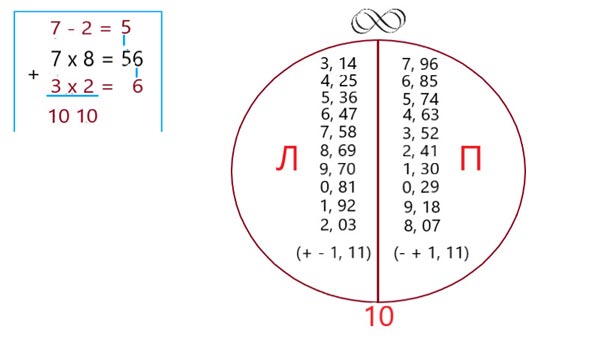
По этому принципу можно создать 20 чисел, свойства которых будут такими же как у числа Пи. На схеме показаны только первые три цифры этих бесконечных чисел (см. рисунок). Между числами имеются вертикальные и горизонтальные каналы связи. Например, количество знаков числа Пи после запятой (июнь 2022 года) составляет около 100 триллионов цифр. Тогда общее количество знаков после запятой у всех 20 чисел достигнет два квадриллиона. В этом гигантском и бесконечном пучковом цифровом образовании может храниться любая информация об окружающем мире на всех языках мира, включая неизвестные.
Все знания, открытые человечеством, могут составлять менее одного процента от объёма, заложенного в их цифровых «архивах». Духовный мир этих чисел делится на две части: реальную (Л) и потустороннюю (П). Каждое из этих чисел имеет своё самостоятельное и бесконечное информационное поле. Цифры на правой стороне показывают незавершённые величины - левой. Подобные явления происходят и в обществе. Например, все действия и упущения правителей, не доведённые до логического завершения, отрицательно влияли на ход событий в истории каждого народа. История не признаёт сослагательного наклонения и всегда пишется на черновике. Числа правой и левой стороны не подлежат сложению. Любая попытка этих действий приводит к блокировке и взаимному уничтожению 20 чисел и всего, что в них находится. В качестве доказательства привожу пример:
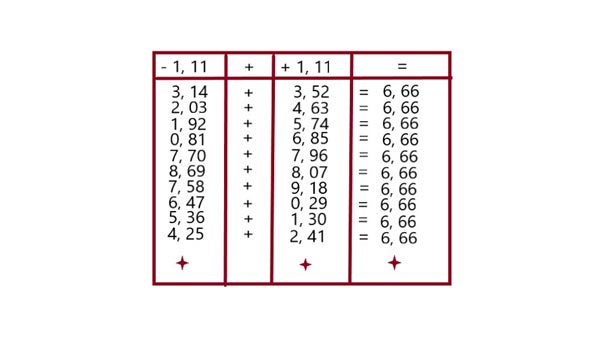
Если в левой части указанной схемы каждую цифру уменьшать на 1, 11, а правую - увеличивать на 1, 11, то в сумме все цифры будут превращаться в шестёрки, или в бесконечное «число зверя». (см. таблицу).
В числе Пи можно найти немало информации, посвящённой числам. Привожу в качестве примера найденные в константе стихи:
«В глубинах чисел мир закрытый,
Хаос мер и бич гурьбы,
Клич времён и дух разлитый,
У моря чисел – пир судьбы.
Ещё корни муз и отзвук веры,
У крыши мира – путь звезды.
В знаках ритма луч играет,
Мыслей бег и грёзы рая.
За ширью мрака ад пылает
И белый шар мерцал у края…»
(Текст взят из числа Пи, 6 млн. 895-я
тысяча цифр после запятой).
Бесконечное число Пи никогда не станет дублировать творческое наследие человечества в его завершённых видах. Проблема состоит в том, что эти сочинения раздроблены на отдельные фрагменты (1 -2 предложения) и разбросаны по всем информационным полям указанных чисел. Их можно собрать только по кусочкам и соединить в единое произведение. Но для этого нужно знать в каких местах они находятся и к какому произведению относятся.
Для эксперимента взял 4 строки стихотворения Сергея Есенина: «Гой ты Русь, моя родная…» и определил местонахождение его строк в числе Пи. В цифровом переводе они расположились так:
«Если крикнет рать святая»: (эта строка присутствует на отрезке – 7 млн. 5-я тысяча цифр после запятой).
«Кинь ты Русь, живи в раю!» - 159-я тысяча.
«Я скажу: не надо рая» - 73-я тысяча.
«Дайте родину мою…» - находится на 1 млн. 995-я тысяче цифр после запятой.
Все 20 бесконечных чисел заполнены полноценными текстами на любую тему. У них нет авторов и деления на фрагменты. Роль человека заключается лишь в поиске, расшифровке и оценке их содержания.
Их творчество ничем не ограничено, никакими правилами и шаблонами. Числа дают информацию о прошлом, настоящем и будущем. Они выполняют роль гигантского хранилища, в котором находятся тексты самого различного содержания. В них возможны любые повороты и глубина мыслей, а также оригинальные идеи. Есть и такие, о которых человечество не догадывается.
Между комбинациями цифр и находящимися в них текстами существует прямая связь. Любая последовательность цифр имеет своё информационное содержание.
Числа способны отражать в теневом виде и творчество известных поэтов. Их расшифровка происходит в потустороннем варианте основного числа, на которое переведено произведение. Для примера я взял известное стихотворение А.С. Пушкина «Свободы сеятель пустынный» (1823 г.). При расшифровке теневого набора цифр этого стихотворения обнаружился параллельный отрывок, который не имеет автора. Привожу их тексты:

По такому же принципу мне удалось расшифровать цифровое отражение строфы L главы VIII романа А.С. Пушкина «Евгений Онегин». Идейному завершению своего романа автор уделял большое внимание. Но его творческие взгляды были ограничены цензурой. Любые намёки в поддержку идей декабристов жестоко карались царской властью. По этим соображениям Пушкин не мог открыто высказывать в романе свои крамольные мысли. Им был найден выход в зашифровке опасных идей методом растворения строк в других текстах и в уничтожении Х главы романа.
Представляю обнаруженный в потустороннем числе текст из завершающей главы:
«Придёт из мрака мыслей след,
Там записи хранят исканий,
Наследие былин и хаос бед,
Передаются дух и грёзы мнений.
Идеи масс о культах из глубин
Забудут: шлейфы, храмы и аллеи,
Замыслы друзей, дары богинь,
Задор плеяды и игру свирели.
А барский век – торги ярма.
Каторга угроза падшим, да тюрьма.К распрям дань у масс созреет,
И бурю их душа затеет…»
Данный текст мог являться отражением духовного мира поэта, или скрытой тенью его творчества. Числа могут хранить в себе и другие виды цифровых творений.
Поединки с числами
«Математику уже затем учить надо,
Что она ум в порядок приводит».
М.В. Ломоносов
Число является основным абстрактным понятием математики. Роль чисел постоянно расширяется, и никто не знает предела их применения. В практике любых количественных вычислений существует множество приёмов, которые помогают в их решении. В достижении результатов многое зависит от исходных данных. Они определяют сложность решения заданий.
В последнее время много внимания уделяется ментальной математике. Быстрый счёт в уме приучает мозг к дисциплине и логике мышления. Он развивает интеллект, память и творческие рамки возможностей человека. Особенно это полезно для учащихся школ и всем, кто увлекается вычислениями в уме на скорость. К сожалению, устный счёт в наших школах практически не применяется. Примеры на умножение чисел решаются учениками, как правило, «столбиком» и в письменном виде.
На уроках математики учащихся с детских лет заставляют заниматься рутинной и механической работой по установленным правилам. Им не нужно сильно напрягать свои мозги, чтобы решать на бумаге подобные примеры. Гораздо больше пользы для развития гибкости мышления и концентрации внимания детей будет при решении двух примеров в уме, чем 20 - в тетради. Возможно, по этой причине у многих учащихся теряется интерес к математике. А этот предмет относится к самой перспективной и таинственной науке в мире. Числа и слова в своей гармонии являются духовными корнями человечества.
В своей практике увлечения математикой я использовал свои приёмы в решении математических примеров. Самыми трудными из них считаю задания на умножение и возведение в степень. В статье показываю только те примеры, которые реально решаются в уме. Каждый из них можно выбирать по своему усмотрению.
читайте также: ключи от Мнемозины
Умножение двузначных чисел
Вариант 1
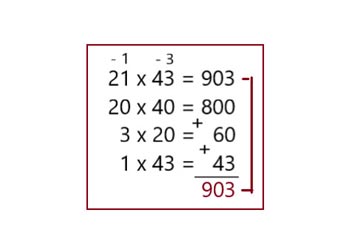
В этом примере множители превращены в десятки, которые легко перемножить. Затем выполняются два действия с цифрами 1и 3. Они решаются в двух вариантах: 1) (3х20) + (1х43) = 103. 2) (3х21) + (1х 40) = 103. Для получения ответа к числу 800 прибавляется 103.
Вариант 2
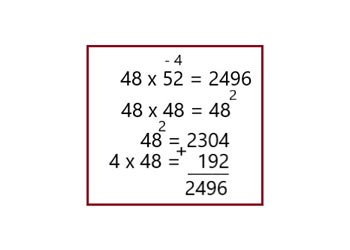
В этом варианте, после изъятия цифры 4 у второго множителя, получаются два одинаковых числа – 48.
Их можно возвести в квадрат. Затем к полученному результату добавляем число 192 и получаем общий ответ.
Вариант 3

Здесь второй множитель уменьшается до числа 11. Любое двузначное число, умноженное на 11, легко решается по схеме: 6 + 8 =14. Эта сумма ставится между
цифрами 6 и 8 и получится – 748.
Вариант 4
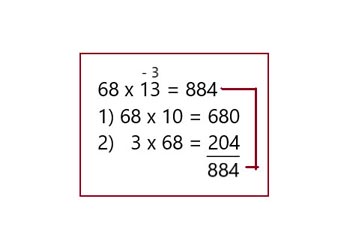
Второй множитель числа превращается в число 10 и перемножается с первым множителем. К результату прибавляем недостающее число 204 и получаем ответ.
Вариант 5
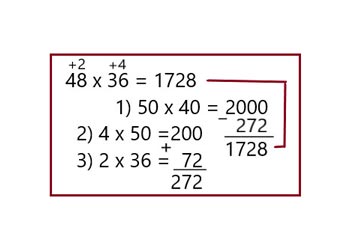
Данный пример решается аналогично первому варианту.
Возведение в квадрат двузначных чисел
Вариант 1
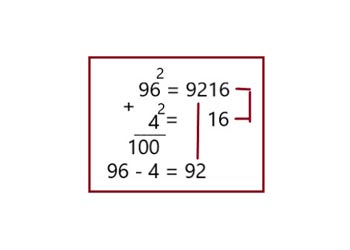
В числе 96 до ста не хватает 4 единицы.
4 в квадрате даёт половину ответа (16).
Если от 96 отнять 4, то получим первую часть ответа.
Вариант 2
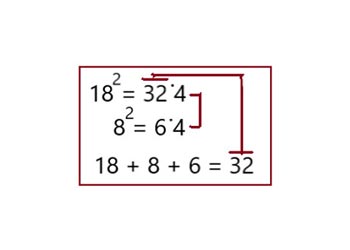
Все числа от 11 до 20 решаются по этой схеме.
Все цифры больше 10 возводятся в квадрат.
Последняя цифра 4 совпадает с концовкой ответа. А его первые две цифры (32) получены от сложения указанных ниже чисел.
Вариант 3

Десятки легче умножать на двузначное число. Поэтому число 67 можно увеличить до 70. А затем из полученного результата отнять число 201 для получения ответа.
это интересно: шаги к разумному человеку
Деление чисел
Вариант 1
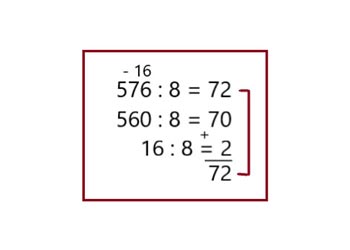
Кроме традиционных методов деления чисел столбиком можно использовать приёмы, показанные в вариантах: 1,2,3. При устном счёте сокращается время на их решение.
Вариант 2
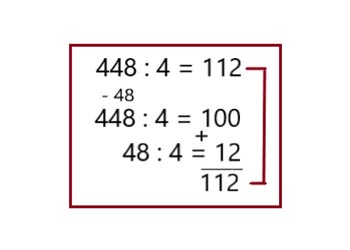
Вариант 3
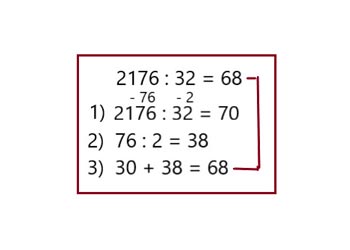
Словесно-цифровая математика
Вариант 1
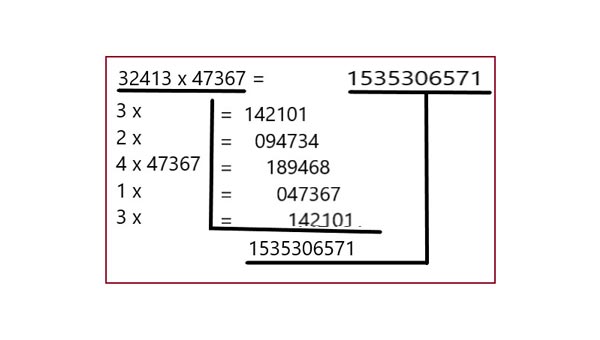
В приведённых ниже вариантах показаны примеры умножения больших чисел. Все они требуют значительной концентрации внимания, чтобы удерживать в памяти ряды цифр и порядок их действий. Показанные ниже приёмы позволяют облегчить их решение. Примером является вариант 1. Во всех остальных случаях можно использовать словесно-цифровой метод. Он состоит в кодировании рядов чисел в тексты. Разработано достаточно много их способов. Самым распространённым является буквенно-цифровой метод, когда каждой цифре присваивается первая буква их названий (7 – С). Из букв этих цифр составляются слова. Их гораздо легче запоминать, чем числа.
Этот метод закрепляется тренировками. Начинать нужно с умножения однозначного числа на многозначное. За результатом любого вычисления должны тянуться отдельные слова, как хвост за кометой. Каждое слово будет заменять 2-3 цифры. Их проще запомнить. Ниже показаны все варианты, где этот метод можно применить.
Вариант 2

Вариант 3

Вариант 4

Вариант 5

Вариант 6
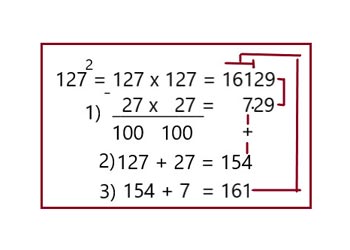
Возведение в квадрат трёхзначных чисел
(приёмы возведения)
Вариант 1

Вариант 2
Вариант 3

Вариант 5
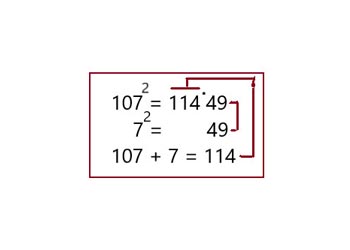
Все 3-значные числа от 100 до 200 решаются простым способом, показанном на схемах вариантов: 5,6,7,8.
Вариант 6
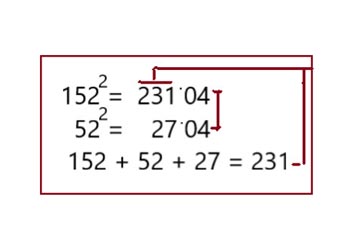
Вариант 7

Вариант 8
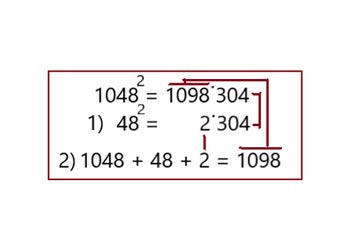
Вариант 9

В этом варианте решение состоит из двух частей. Вначале из 10000 выделяется число 132 и возводится в квадрат. В результате получим пять цифр, 4 из которых относятся к концовке общего ответа. Во второй части решения из 100 выделяем число 32 и возводим его в квадрат и далее решаем по такой же схеме.
связанная статья: находки в дебрях константы
Таблица квадратов чисел
В математике широко применяется таблица умножения, которую учат все. Не менее важна и таблица квадратов двузначных чисел. Если убрать из неё десятки, то количество примеров сократится до 81. Её всю можно закодировать в слова. Тогда каждый пример будет состоять из 2-3 слов. Одно слово будет принадлежать числу, которое будет возводиться в степень, а 1-2 – ответу. Последнюю цифру ответа включать не нужно. На запоминание этой словесно-цифровой таблицы потребуется немного времени. Я выучил её за 3 часа.
Она позволяет решать квадраты этих чисел мгновенно и выдавать ответ за 2-3 секунды. Эту таблицу может составить любой желающий, по схеме, которую предлагаю ниже. Из своей таблицы выбрал 7 примеров, которые показались мне более интересные.

Знание таблицы квадратов позволяет быстро решать в уме приведённые ниже примеры (варианты 1,2,3).
Вариант 1
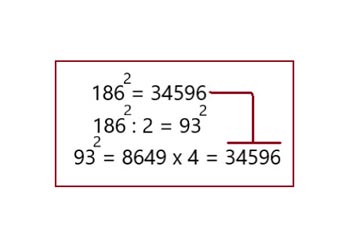
Вариант 2

Вариант 3
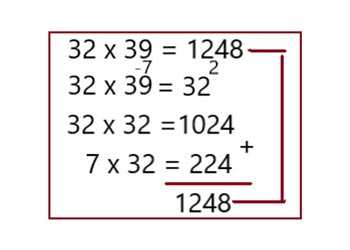
Универсальный алгоритм решений
При умножении многозначных чисел в уме многие примеры даже математики считают не подъёмными. Например, немногие могут умножить в уме числа из 7-10 знаков. В настоящее время мировой рекорд по умножению 10-значных чисел в уме принадлежит России. Пример был решён за 14 минут 31 секунду.
Человек давно научился обращаться с неподъёмными грузами. Он использует для этого два способа: 1. Применяет рычаг. 2. Делит груз на части и переносит его. В математике вместо рычага к большим числам обычно применяют письменный метод.
Умножение чисел, как правило, считается единым процессом и на отдельные самостоятельные части не дробится. Например, если всю операцию при умножении 5-значных чисел разделить на 10 отдельных частей, то их решение облегчится в 10 раз! На каждую цифру ответа будет проводиться отдельное вычисление. Такой метод позволит любому человеку решать подобные примеры в уме без особых усилий. Для этого требуется разработка универсального алгоритма действий для каждого знака ответа. Количество алгоритмов решений будет равно количеству знаков в ответе.
При освоении этой методики не будет считаться фантастикой умножение в уме 15-значных чисел. В ответе будет 30 знаков, которые потребуют 30 отдельных цифровых решений. Алгоритмы на каждое решение можно реально запомнить и применять их каждый раз в уме. По такой же методике можно разработать алгоритм возведения двузначного числа в 10-ю и более высокую степень. И такие возможности в практике имеются.
Разработать и усвоить универсальные алгоритмы решений любых чисел можно по образцу умножения двузначных чисел. Например, 12 х 34 = 1234. На схеме результаты умножений каждой пары цифр помечены знаками: десятки – 0, а единицы – 1. В центре образовались два столбика из трёх цифр, которые складываются.
Например, чтобы получить третью цифру ответа нужно перемножить 3 пары цифр: 3х4(1), 8х4(0) и 8х6(1). В скобках указаны значения единиц и десятков, которые складываются. 2(1) + 3(0) + 8(1) =3. Такие же действия проводятся для вычисления 2-й цифры ответа. Если оба множителя обозначить номерами (1234), то получится алгоритм решения при умножении любых двузначных чисел (см. правую сторону схемы).
Вариант 1
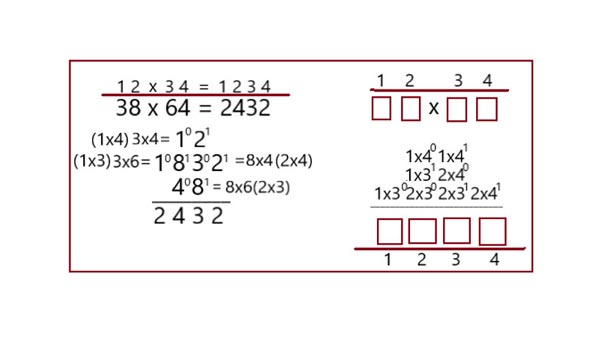
Вариант 2
Во втором варианте показан алгоритм решения, когда множители обозначаются буквами (ab).

Таким же способом можно разработать и запомнить алгоритмы решений при умножении других чисел. Каждый пример по этой методике будет быстро решаться в уме.
Автор: Владимир Кондряков





